zhongjzsb

Chapter 1.5 Fixed Income Securities

 
  • Jingyu Bao
  • Jun 28, 2015

Chapter 1.5 Fixed Income Securities

Description

From chpater 3 in Statistics and Data Analysis for Financial Engineering (David Ruppert).

For semiannual coupon,

#  Program to create Fig 3.2
bondvalue = function(c,T,r,par)
{
#
#   Computes bv = bond values (current prices) corresponding
#       to all values of yield to maturity in the
#       input vector r
#
#       INPUT
#        c = coupon payment (semi-annual)
#        T = time to maturity (in years)
#        r = vector of yields to maturity (semi-annual rates)
#        par = par value
#
bv = c/r + (par - c/r) * (1+r)^(-2*T)
bv
}
################################

#   Computes the yield to maturity of a bond paying semi-annual
#   coupon payments
#
#   price, coupon payment, and time to maturity (in years)
#   are set below
#
#   Uses the function "bondvalue"
#
price = 1200    #   current price of the bond
C = 40          #   coupon payment
T= 30           #   time to maturity
par = 1000      #   par value of the bond

r = seq(.02,.05,length=300)
value = bondvalue(C,T,r,par)
yield2M = spline(value,r,xout=price)

plot(r,value,xlab='yield to maturity',ylab='price of bond',type="l",
    main="par = 1000, coupon payment = 40, T = 30",lwd=2)
abline(h=1200)
abline(v=yield2M)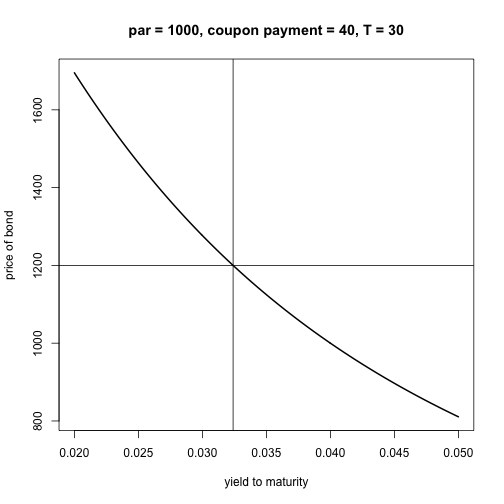

center

################
#  Finding r from the price using a root finder

uniroot(function(r) bondvalue(C,T,r,par) - price, c(0.001,.1))
## $root
## [1] 0.03240908
##
## $f.root
## [1] -0.3334967
##
## $iter
## [1] 6
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05

Problem 3 Use uniroot to find the yield to maturity of the 30-year par $1000 bond with coupon payments of $40 that is selling at $1200.

T = 30
C = 40
par = 1000
price = 1200
uniroot(function(r) bondvalue(C,T,r,par) - price, c(0.001,.1))
## $root
## [1] 0.03240908
##
## $f.root
## [1] -0.3334967
##
## $iter
## [1] 6
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05

Problem 4 Find the yield to maturity of a par $10,000 bond selling at $9800 with semiannual coupon payments equal to $280 and maturing in 8 years.

T = 8
C = 280
par = 10000
price = 9800
uniroot(function(r) bondvalue(C,T,r,par) - price, c(0.001,.1))
## $root
## [1] 0.02959024
##
## $f.root
## [1] -0.3783491
##
## $iter
## [1] 4
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 0.0001175906

Exercises

Problem 1.

Suppose that the forward rate is $r(t) = 0.028 + 0.00042t$.

[a]. What is the yield to maturity of a bond maturing in 20 years?

[b]. What is the price of a par $1000 zero-coupon bond maturing in 15 years?

Answer:

[a]. Using the formula

r <- function(t){0.028 + 0.00042*t}
yield <- prod(1 + r(c(1:20)))^(1/20) - 1

The yield to marturity of a bond maturing in 20 years is 0.0324072.

[b]. The price is par dividing the forward rate at each year.

P_15 <- 1000/prod(1 + r(c(1:15)))

Therefore, the price of a par $1000 zero-coupon bond maturing in 15 years is 629.2972379.

Problem 2.

A coupon bond has a coupon rate of 3% and a current yield of 2.8%.

[a]. Is the bond selling above or below par? Why or why not?

[b]. Is the yield to maturity above or below 2.8%? Why or why not?

Answer:

[a]. Following the figure above, if the coupon rate is 3% and current yield is 2.8%, i.e. coupon rate (coupon/par) is larger than current yield (coupon/current price), par is less than current price. Then, the bond is selling above par.

[b]. The yield to maturity is below 2.8%. Because current yield is always bewteen coupon rate and yield to maturity. Because

PAR is larger than C/r. The price gets larger when T gets larger. Therefore, the current yield will goes down, and the yield to maturity, the average of yields, will below current yield.

Problem 3.

Suppose that the forward rate is $r(t) = 0.032 + 0.001t + 0.0002t^2$.

[a]. What is the five-year continuously compounded spot rate?

[b]. What is the price of a zero-coupon bond that matures in five years?

Answer:

[a]. Let $t=5$

[b]. Using formula

Search